Stacked Polarizers
I've been reading these quantum mechanics slides. The stacked polarizer example is interesting. Before I explain the example, let me explain polarized filters first.
A photon, light ray, will pass through a polarized filter if the photon's polarization is perfectly aligned with the filter, but the photon will be absorbed by the filter if it's perfectly unaligned. If the photon is partially aligned, either case can happen, but the closer the photon's polarization is to the filter's, the more likely the photon will pass through. More interestingly, any photon that passes through will assume the polarity of the filter. Twenty filters aligned perfectly have the same effect as one filter. If the photon enters through the first filter, it is guranteed to pass through the rest.
You can reproduce these results with common household items. If you haven't gotten a chance, please go find some sunglasses or filter plastic to play with. Hint: your computer monitor emits polarized light. Question: How can you see a screen with polarized sunglasses on. What happens if you turn your head or screen sideways?
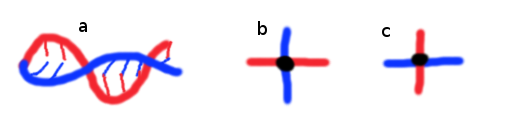
Figure 1: Three images of a photon. The blue wave is the electric field wave. The red wave is the magnetic wave. Image a. shows the two waves of a photon, light ray, propogating forward. Image b. shows the wave head on. Image c. shows the wave head on, but with a different polarization. In c., the wave has been rotated around its direction of propogation.
The lecture note example describes a series of slightly offset polarizers. Each polarizer is slightly unaligned with the previous polarizer. Intuitively, a photon has a high chance of passing through the first filter. After passing, the photon will be aligned with the filter. Interestingly, the photon is always out of alignment by the same amount. In practice, the odds of going through every filter quickly plummets.
In the example, the polarity between filters is not kept constant offset. Instead, the sum of the offsets is always a cosntant. Put another way, any photon that makes it all the way through a 10 stack filter will have the same polarization as a photon that makes it through a 100 stack filter. The rotation is always by the same amount.
The equation below calculates the probability. The outer exponentation corresponds to the amount of filters. The inner expression corresponds to the probablity of passing through a single filter. As the amount of filters increases, the turn of each filter decreases.
 1
1
import math
def foo(n):
return (math.cos(math.pi) ** 2) ** n
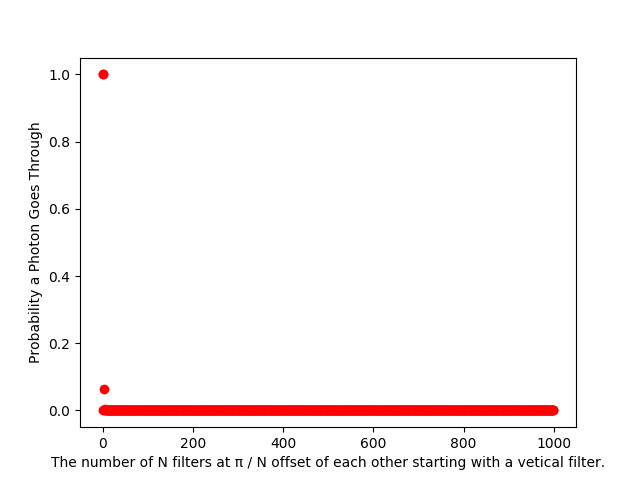
In the original example, the total rotation is  ; a photon that exits the last filter experiences a
; a photon that exits the last filter experiences a  phase shift. Below is a graph plotting the probability of a photon passing through every filter. The first dot is no filters and the second dot is one perfectly aligned filter. The pass rate drops off rapidly as filters are added. Interestingly, the drop is near immediate.
phase shift. Below is a graph plotting the probability of a photon passing through every filter. The first dot is no filters and the second dot is one perfectly aligned filter. The pass rate drops off rapidly as filters are added. Interestingly, the drop is near immediate.
This seems to be related to the total turn rate value,  . Using a smaller turn rate, the pass rate dives slowly.
. Using a smaller turn rate, the pass rate dives slowly.
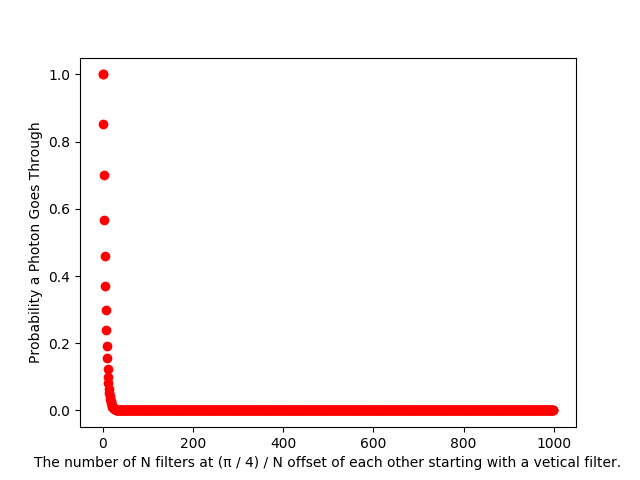
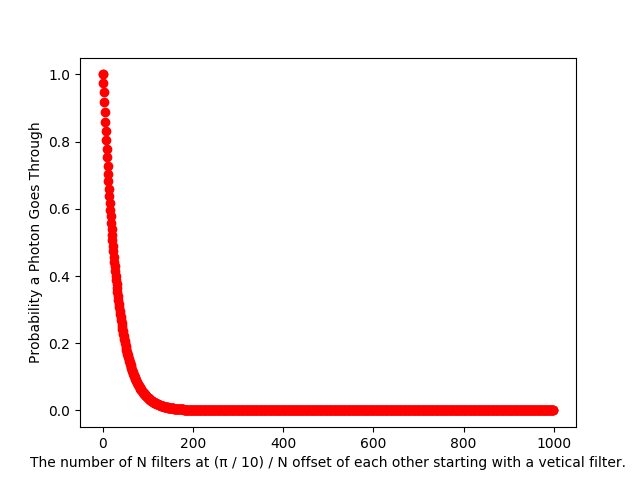
I'm still confused with the blip at three filters, two offsets, in the first graph. I can't tell if that's a weird floating point error, some math quirk, or an error on my part.
Code for generating the graphs:
import math
import numpy as np
import matplotlib.pyplot as plt
VERTICAL_BASIS = np.array([1, 0])
HORIZONTAL_BASIS = np.array([0, 1])
BASIS_SET = [VERTICAL_BASIS, HORIZONTAL_BASIS]
def is_orthogonal(basis_set):
return all(np.dot(first, second) == 0
for first in basis_set
for second in basis_set
if (first != second).all()
)
is_orthogonal([VERTICAL_BASIS, HORIZONTAL_BASIS])
def is_normal(basis):
return 1 == basis.dot(basis)
def is_orthonormal(basis_set):
return is_orthogonal(basis_set) and all(map(is_normal, basis_set))
def make_polarizer(theta):
return np.array([math.cos(theta), math.sin(theta)])
def apply_polarizer(ket, polarizer):
return {
'rate' : ket.dot(polarizer) ** 2,
'state': polarizer
}
def generate_stacked_polarizers(iterations, total_turn):
if iterations == 0:
return []
step_size = total_turn / iterations
return [
make_polarizer(step_size * step)
for step in range(iterations)
]
def apply_polarizers(ket, polarizers):
rate = 1
state = ket
for polarizer in polarizers:
result = apply_polarizer(ket, polarizer)
rate *= result['rate']
state = result['state']
return {
'rate': rate,
'state': state
}
def generate_stacked_polarizer_graph(iterations, total_turn, offset_label):
results = [
apply_polarizers(
VERTICAL_BASIS,
generate_stacked_polarizers(
iterations=i,
total_turn=total_turn
)
)
for i in range(iterations)
]
plt.plot([datum['rate'] for datum in results], 'ro')
plt.ylabel('Probability a Photon Goes Through')
plt.xlabel('The number of N filters at {} / N offset of each other starting with a vetical filter.'.format(offset_label))
plt.show()
generate_stacked_polarizer_graph(1000, math.pi, 'π')
generate_stacked_polarizer_graph(1000, math.pi / 4, '(π / 4)')
generate_stacked_polarizer_graph(1000, math.pi / 10, '(π / 10)')