Inversion About the Average
Inversion about the average is a way of converting phase differences into magnitude differences. It is simple to understand, easy to implement, and a key part of Grover's Algorithm, the quantum search algorithm.
Set Up
Suppose we have a state vector. Each component is a probability amplitude.
import math import numpy as np # There are 4 possible outcomes and each has a 25% chance of occurring P_V = np.array([1, 1, 1, 1] / math.sqrt(4))
To get the probability of measuring a state, we multiply the probability amplitude by its complex conjugate.
def calculate_probabilities(amplitudes):
return [amplitude * amplitude.conjugate() for amplitude in amplitudes]p
Each state corresponds to one of the possible outcomes, so the sum of the square of the probability amplitudes must be unity, 100%.
 1
1
In our state vector, every outcome is equally likely. The state probability amplitudes and state probabilities can be represented, respectively, by the graphs in figure 1 and figure 2
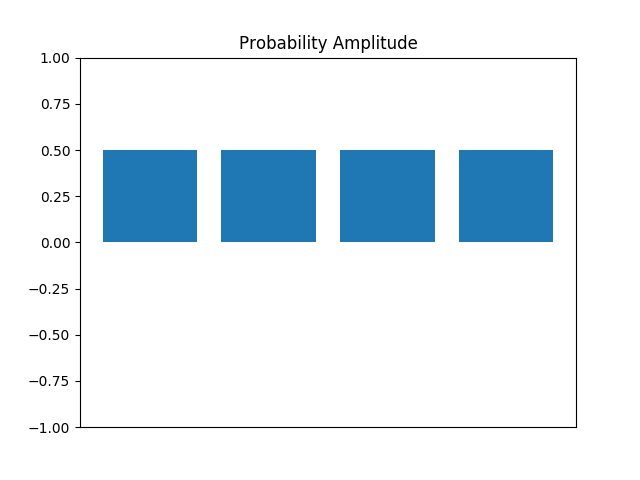
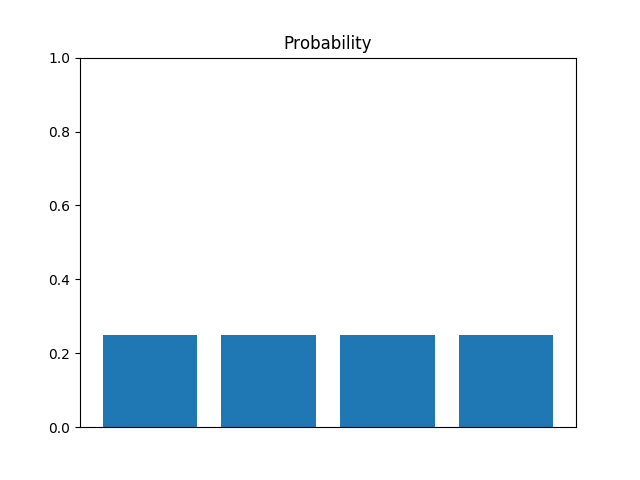
Suppose we had a way to flip the state we want to measure, a selective phase flip. If the state we want to measure is the third state, for example, then we would have the following vector.
# There are 4 possible outcomes and each has a 25% chance of occurring P_V = np.array([1, 1, -1, 1] / math.sqrt(4))
The corresponding measurements are seen in figure 3 and figure 4.
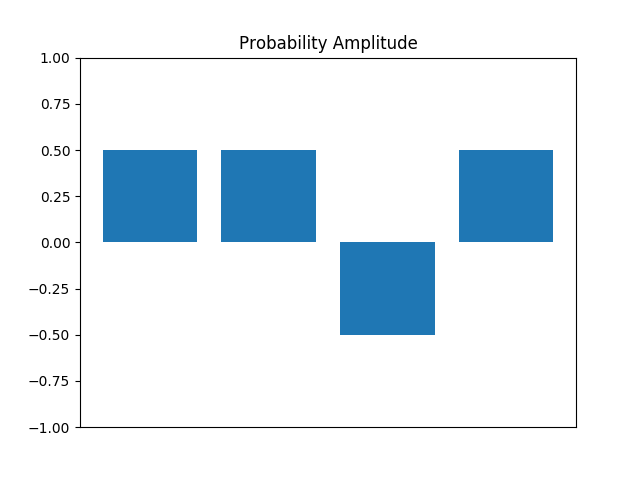
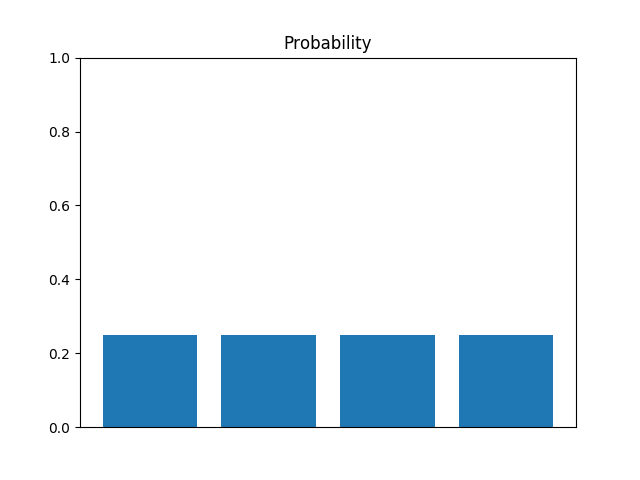
We can perform a selective phase flip using unitary operations, but that's outside the scope of this blog post. For now, lets just assume we can.
Note that even with the phase flip, each state still has a 25% probability of being measured. It's as if we made no change at all, but that's not true. Inversion about the average allows us to transform a difference in phase into a difference in magnitude.
Inversion About the Average
As noted by Noson S. Yanofsky and Mirco A. Mannucci in Quantum Computing for Computer Scientists, an average can be geometrically interpreted as "the number such that the sum of the lengths of the lines above the average is the the same as the sum of the lengths of the lines below."
Try it Again
We can repeat the operation to increase the magntiude more. Unfortunately, we can over do it. Performing phase shifts and then average around the mean will at first raise the magnitude of our goal, but will eventually decrease the magnitude.
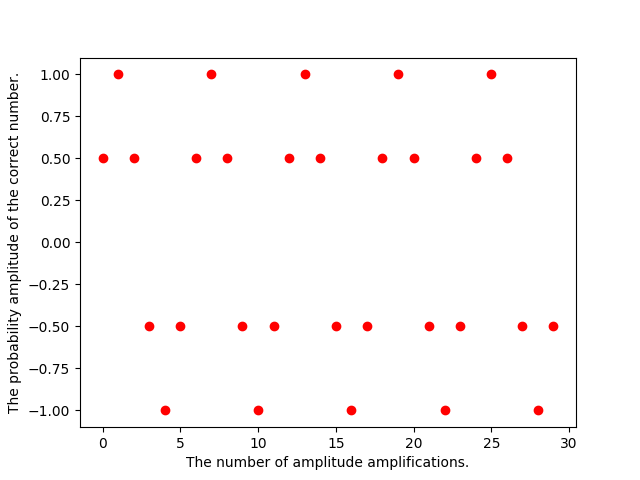
The pattern is cyclical. It follows the pattern of a sin wave. The following equaiton gives how many points are required to land on a peak:
 2
2
 is the number of iterations,
is the number of iterations,  is the size of the search space and
is the size of the search space and  is the number of correct answers. This equation, however, assumes
is the number of correct answers. This equation, however, assumes  . For our example, this doesn't hold; there's only four inputs. I've fudged the
. For our example, this doesn't hold; there's only four inputs. I've fudged the  wave to make it match the input values as close as I can. The periodicity of inversaion about the average should be clear.
wave to make it match the input values as close as I can. The periodicity of inversaion about the average should be clear.
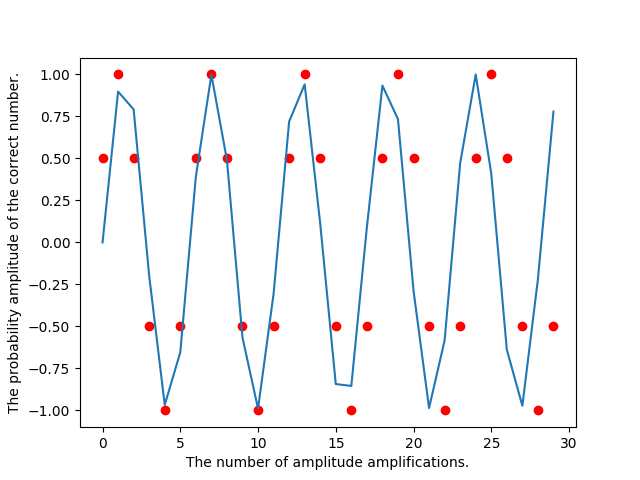
Outro
In this article, I described inversion about the average using code samples and visuals. Inversion about the average is periodic; too many applications will reverse the effects.