Fast Compilation with Lisp
While reading about finite automata and regular languages, I realized something: compilation is faster than interpretation, but programming languages are a specific case of interpretation and compilation.
Put another way, compilers and interpreters are two ways of handling an abstract syntax tree. The interpreter is data structure driven: it follows the abstract syntax tree performing actions as it goes. The compiler is also data structure driven: it takes an abstract syntax tree and converts it to an executable. The key insight is that an abstract syntax tree is a special case. Any data structure driven program is either an interpreter or a compiler.
As an example, consider the scanner in compilers. The job of the scanner is to split the source code text stream into tokens for the parser. There are two ways to implement the scanner: one is to hand code the fastest scanner you can; the other is to identify the regular expressions describing the language, compile the regular expressions into a table, and then use the table to drive the scanner. It is common knowledge that hand written scanners are faster than table driven scanners. [Programming languages] However, this seems to be a false dichotomy. There's a third option.
In a compiler, the scanner acts as a kind of compiler itself. It takes a stream of text and creates tokens. Then, the parser acts as a kind of compiler, it takes the stream of tokens and returns an abstract syntax tree. I use compiler to mean a transformation on static data: a transformation that can be done on input known ahead of time. It's hard to imagine a scanner or parser that works differently.
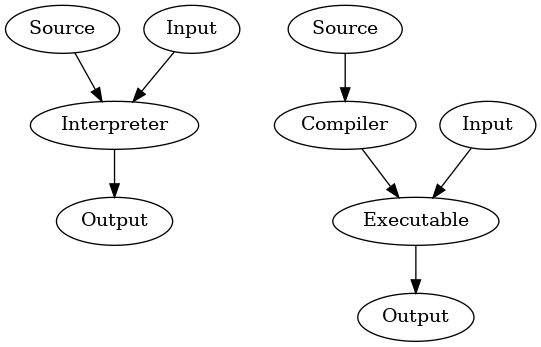
Figure 1: An interpreter takes program input and source code at the same time. A compiler translates program input into an optimized executable and then maps input to output.
A scanner, a tool that transforms a regular language into a table is a kind of compiler itself. It takes a stream of text and creates tokens. But how is the table handled? In a table driven scanner, the table is interpreted. A program walks the table to handle a stream of source code. The obvious question is "If the table is constant, why not compile the table?"
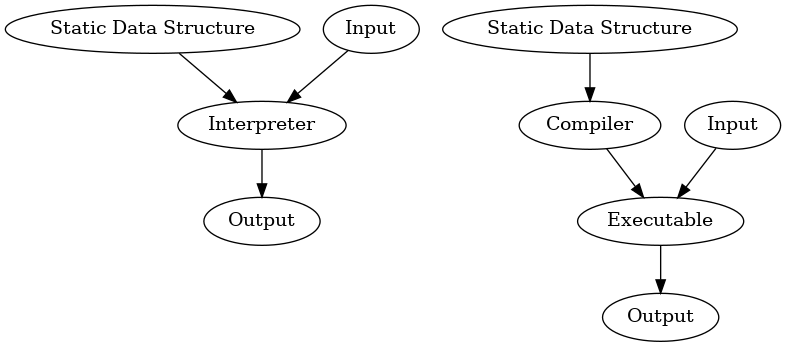
Figure 2: Walking a static data structure is like interpreting a programming language, slow and easy.
This has been done. Consider Doug Hoyte's description of Edi Weitz's Common Lisp regular expression library:
[…] CL-PPCRE is fast. Really fast. When compiled with a good native code compiler, benchmarks suggest that for most regular expressions CL-PPCRE is roughly twice as fast as Perl, often much faster. And Perl has one of the fastest non-lisp regular expression engines around: a highly optimised engine written in C. How is this possible? Surely Perl's low-level implementation should have a performance edge over anything written in a high-level language like lisp.
Let Over Lambda, Chapter 4, Doug Hoyte
My guess is that Edi is compiling regular expressions into a table and compiling the resulting table. While this seems difficult, compiling code in Lisp is very easy. All you have to do is walk the data structure and build up a large lambda. Paul Graham's On Lisp includes a chapter where Paul Graham compiles a decision tree.
By representing the nodes as closures, we are able to transform our twenty-questions network entirely into code. As it is, the code will have to look up the node functions by name at runtime. However, if we know that the network is not going to be redefined on the fly, we can add a further enhancement: we can have node functions call their destinations directly, without having to go through a hash-table.
The end of the chapter sums up the basic idea.
"To represent with closures" is another way of saying "to compile,"
To make our system faster, we'll hand generate jumps using Common Lisp's support for goto.
Example
To make my point, I created a small library working with finite state machines. There are two ways to use a state machine with my library: the finite state machine can be interpreted with the scan method and the finite state machine can be compiled directly into a two tier jump table. To show the distinction between the two methods I'll need an example state machine, example input, and then a measurement of each case.
My finite state machine is an example taken from Sisper.

Figure 3: This finite state machine tracks a bounded position state. The u can be interpreted as "Up". The d can be interpreted as "Down".
Below, I define a FSM equivalent to the state diagram. I start by defining the state-transition function with a hash table and then I create an object containing the start state, alphabet, list of states, end states, and transition table.
(defparameter *transition-table-example-2* (make-hash-table :test #'equalp)) (let ((table *transition-table-example-2*)) (setf (gethash #(base #\u) table) 'u) (setf (gethash #(base #\d) table) 'd) (setf (gethash #(u #\u) table) 'uu) (setf (gethash #(u #\d) table) 'base) (setf (gethash #(d #\u) table) 'base) (setf (gethash #(d #\d) table) 'dd) (setf (gethash #(uu #\u) table) 'uuu) (setf (gethash #(uu #\d) table) 'u) (setf (gethash #(uuu #\u) table) 'uuu) (setf (gethash #(uuu #\d) table) 'uu) (setf (gethash #(dd #\u) table) 'd) (setf (gethash #(dd #\d) table) 'ddd) (setf (gethash #(ddd #\u) table) 'dd) (setf (gethash #(ddd #\d) table) 'ddd)) (defparameter *automata-example-2* (make-instance 'finite-automata :start-state 'base :alphabet (list #\u #\d) :states (list 'base 'u 'd 'uu 'dd 'uuu 'ddd) :end-states (list 'base) :transition-table *transition-table-example-2*))
Next, I need some input. Random input should be fine, so I'll generate a random sequence of 1000 valid characters.
(defparameter *inputs-example-1*
(flet ((random-input ()
(aref #(#\u #\d) (random 2))))
(coerce (loop for i below 1000
collect (random-input))
'string)))
The input is shown below.
"uuududdduddduududududddduuudududduudddduuududududuuduuuuuduudduuuuuuddduddduduuuudduudududduudduuduudduduududduuduuuuduuudddddddudduuuuduuuduuuudududdduduudddddddduuuddduduuuudduddduuuduuuudduuduudddddududududduuuduuuududdddduuuuuuduududuuuduuuuuduuddduududuududuududduddududduuuuuududududuuuduuududduudddddddduududduuuudddduuuuduuuddddududduudduduuudddddudddddddduuuuduudddddududduudduuuududuuduuuduudduuuuddddudduddduddudduduuududddduddduudduuduuuuddduuuudduduudduuduududduuuduuudddduddduuuuuudduddududddduuududddudddudddudduuduuduuddduddudddduuudduudduduuduuddduudduduududduuddudduduudddddduududuuuuuddduudddduddudddddddduduuduuduududdduddduddduudduduuuuuduuuduuuddududuuuddddddddduuddudduududdddududuudddduuudduudduuduuududuudduduuuuudududuuududdudduduuudduuuudududduddduuuuududuuudddddduuuuuuddduududduudduuuuuduuuuduududuudududuudduuuuduuuddududuuuudduuuududdddduuduuddudduuddduududdududuuduuddduuuudduuudddduddddduuuuuudduudddudduuudududuuduudddddduudduduuddudududdududuuddddduduuuudduuududuuu"
I can benchmark the code using the trival-benchmark package.
(ql:quickload 'trivial-benchmark) (benchmark:with-timing (10) 'test)
This results in the following output:
- SAMPLES TOTAL MINIMUM MAXIMUM MEDIAN AVERAGE DEVIATION REAL-TIME 10 0 0 0 0 0 0.0 RUN-TIME 10 0 0 0 0 0 0.0 USER-RUN-TIME 10 0 0 0 0 0 0.0 SYSTEM-RUN-TIME 10 0 0 0 0 0 0.0 PAGE-FAULTS 10 0 0 0 0 0 0.0 GC-RUN-TIME 10 0 0 0 0 0 0.0 BYTES-CONSED 10 0 0 0 0 0 0.0 EVAL-CALLS 10 0 0 0 0 0 0.0 NIL
With an example state machine, test input, and a benchmark tool, we can now compare interpretation to compilation.
Table Driven Interpreter
The table driven interpreter uses the scan method to walk the table until the input is exhausted.
(benchmark:with-timing (100000)
(with-input-from-string (input *inputs-example-1*)
(scan *automata-example-2* input)))
The timing results are below:
- SAMPLES TOTAL MINIMUM MAXIMUM MEDIAN AVERAGE DEVIATION REAL-TIME 100000 12.187 0 0.016 0 0.000122 0.000351 RUN-TIME 100000 12.208 0 0.012 0 0.000122 0.000692 USER-RUN-TIME 100000 12.036 0 0.012 0 0.00012 0.000688 SYSTEM-RUN-TIME 100000 0.184 0 0.004 0 0.000002 0.000086 PAGE-FAULTS 100000 0 0 0 0 0 0.0 GC-RUN-TIME 100000 0.276 0 0.012 0 0.000003 0.00013 BYTES-CONSED 100000 3214350368 0 1142480 32768 32143.504 5735.312 EVAL-CALLS 100000 0 0 0 0 0 0.0
Compiled Table
The compiler transforms the automata table to machine code. The transformation is done outside of the benchmark timing, because it can be done at compile time; the compiled automata is reused each time. Unlike the table driven interpeter, the method scan is not used. The compile creates a lambda that can be called with funcall.
(let ((scanner (eval (compile-automata *automata-example-2*))))
(benchmark:with-timing (100000)
(with-input-from-string (input *inputs-example-1*)
(funcall scanner input))))
The dissasembly of the scanner function can be seen below.
(let ((scanner (eval (compile-automata *automata-example-2*)))) (disassemble scanner))
The timing results are below:
- SAMPLES TOTAL MINIMUM MAXIMUM MEDIAN AVERAGE DEVIATION REAL-TIME 100000 1.606 0 0.012 0 0.000016 0.000131 RUN-TIME 100000 1.596 0 0.012 0 0.000016 0.000254 USER-RUN-TIME 100000 1.424 0 0.012 0 0.000014 0.00024 SYSTEM-RUN-TIME 100000 0.196 0 0.004 0 0.000002 0.000089 PAGE-FAULTS 100000 19 0 3 0 0.00019 0.016431 GC-RUN-TIME 100000 0.012 0 0.012 0 0.0 0.000038 BYTES-CONSED 100000 12953552 0 130960 0 129.53552 2090.5718 EVAL-CALLS 100000 0 0 0 0 0 0.0 NIL
Conclusion
The compiled version is ~10 times faster, but the compiler implementation is less than 20 lines of code.
(defun compile-automata (automata)
(let ((escape (gensym "ESCAPE-"))
(eof-value (gensym "EOF-VALUE-")))
`(lambda (input)
(declare (optimize (safety 0) (speed 3)))
(block ,escape
(tagbody
,@(loop for state in (states automata)
append (list state
`(ecase (read-char input nil ',eof-value)
,@(loop for input in (alphabet automata)
collect `(,input (go ,(gethash (vector state input) (transition-table automata)))))
(',eof-value (return-from ,escape ',state))))))))))
The compiler is a dense. An example will help explain what happens. The output of compiling the example state machine is shown below.
(LAMBDA (REGULAR-LANGUAGE-COMPILER::INPUT)
(DECLARE (OPTIMIZE (SAFETY 0) (SPEED 3)))
(BLOCK #:ESCAPE-726
(TAGBODY
BASE
(ECASE (READ-CHAR REGULAR-LANGUAGE-COMPILER::INPUT NIL '#:EOF-VALUE-727)
(#\u (GO U))
(#\d (GO D))
((QUOTE #:EOF-VALUE-727) (RETURN-FROM #:ESCAPE-726 'BASE)))
U
(ECASE (READ-CHAR REGULAR-LANGUAGE-COMPILER::INPUT NIL '#:EOF-VALUE-727)
(#\u (GO U))
(#\d (GO BASE))
((QUOTE #:EOF-VALUE-727) (RETURN-FROM #:ESCAPE-726 'U)))
D
(ECASE (READ-CHAR REGULAR-LANGUAGE-COMPILER::INPUT NIL '#:EOF-VALUE-727)
(#\u (GO BASE))
(#\d (GO DD))
((QUOTE #:EOF-VALUE-727) (RETURN-FROM #:ESCAPE-726 'D)))
UU
(ECASE (READ-CHAR REGULAR-LANGUAGE-COMPILER::INPUT NIL '#:EOF-VALUE-727)
(#\u (GO UUU))
(#\d (GO U))
((QUOTE #:EOF-VALUE-727) (RETURN-FROM #:ESCAPE-726 'UU)))
DD
(ECASE (READ-CHAR REGULAR-LANGUAGE-COMPILER::INPUT NIL '#:EOF-VALUE-727)
(#\u (GO D))
(#\d (GO DDD))
((QUOTE #:EOF-VALUE-727) (RETURN-FROM #:ESCAPE-726 'DD)))
UUU
(ECASE (READ-CHAR REGULAR-LANGUAGE-COMPILER::INPUT NIL '#:EOF-VALUE-727)
(#\u (GO UUU))
(#\d (GO UU))
((QUOTE #:EOF-VALUE-727) (RETURN-FROM #:ESCAPE-726 'UUU)))
DDD
(ECASE (READ-CHAR REGULAR-LANGUAGE-COMPILER::INPUT NIL '#:EOF-VALUE-727)
(#\u (GO DD))
(#\d (GO DDD))
((QUOTE #:EOF-VALUE-727) (RETURN-FROM #:ESCAPE-726 'DDD))))))
This goto laden code is a two tier jump table.
An example of the same state machine hand written is below.
(with-input-from-string (input *inputs-example*)
(symbol-macrolet ((value (read-char input nil 'eof-value)))
(block escape
(tagbody
base (ecase value
(#\u (go u))
(#\d (go d))
(eof-value (return-from escape 'base)))
u (ecase value
(#\u (go uu))
(#\d (go base))
(eof-value (return-from escape 'u)))
d (ecase value
(#\u (go base))
(#\d (go dd))
(eof-value (return-from escape 'd)))
uu (ecase value
(#\u (go uuu))
(#\d (go d))
(eof-value (return-from escape 'uu)))
dd (ecase value
(#\u (go d))
(#\d (go ddd))
(eof-value (return-from escape 'dd)))
uuu (ecase value
(#\u (go uuu))
(#\d (go uu))
(eof-value (return-from escape 'uuu)))
ddd (ecase value
(#\u (go dd))
(#\d (go ddd))
(eof-value (return-from escape 'ddd)))))))
To write the compiler, I first hand wrote this state machine. Then, I wrote the compiler.
The benchmark results are impressive, but the interpreter is very slow. It uses a hash table rather than a 2D array. An interpreter that translates states and inputs to array indices might perform better. On the other hand, a better interpreter might be more complicated than my simple compiler.